---

ÉNERGIE DE LA VAPEUR D'EAU (suite)

Applications aux machines

Cycle machine à vapeur 20b

Machine parfaite (cycle de Hirn)

Examinons le diagramme T S d'une machine à vapeur (cf diagrammes ci dessous) :
Du point 1 au point 2 : production de la vapeur (chauffage de l'eau jusqu'à 212°C, puis évaporation : trait vert horizontal, puis chauffage de la vapeur jusqu'à 400°C : surchauffe). La surface sous la courbe indique la quantité de chaleur nécessaire.
Du point 2 au point 3 : la vapeur se détend dans une machine parfaite (pas de frottements ni de perte de chaleur) jusqu'à la pression de 120 mb (50°C) du condenseur en fournissant du travail. Pour cette machine parfaite la transformation suit une verticale (S ne change pas). Bien entendu aucune machine réelle ne peut faire mieux.
Le point 3 est à gauche de la ligne bleue, donc en fin de détente il y a mélange eau/vapeur.
Du point 3 au point 1 : la vapeur se condense dans le condenseur à 50°C. La surface sous la courbe indique la quantité de chaleur à évacuer.
Pour finir le cycle, il faut pomper l'eau du condenseur vers la chaudière (l'énergie nécessaire est faible comparée aux autres : épaisseur du trait)

Chaleur dépensée pour produire la vapeur (hachures rouges)

Chaleur perdue dans le condenseur (hachures bleues) Travail de la vapeur récupéré par la machine (hachures vertes)

Pour un cycle on voit l'énergie dépensée (rouge), l'énergie perdue (bleue) et le travail récupéré (vert) qui est la différence des 2. Ce travail s'appelle travail indiqué. C'est le travail fourni par la vapeur, sans tenir compte du rendement mécanique (frottement) ni de celui de la chaudière.
Il peut être calculé, sur une machine réelle à piston, à partir du diagramme de Watt (mesure de la pression en fonction de la position du piston) : c'est la surface de ce diagramme pression*volume.

Augmentation du rendement :

1 - augmenter la pression de la chaudière : la ligne 1 - 2 remonte, le travail récupéré augmente (le rendement aussi même si la chaleur dépensée augmente)
2 - baisser la pression du condenseur : la ligne 1 - 3 baisse, le travail récupéré augmente. (Exemple machine du Titanic : la turbine qui ne fonctionne que de 0,6 à 0,07 bars fournit une puissance égale à 60% de celle des machines à pistons triple expansion qui utilisent pourtant la vapeur de 15 à 0,6 bars. Voir page machines).

Mais quand on baisse la pression du condenseur, le point 3 se trouve plus à l'intérieur de la courbe bleue : il y a un pourcentage de vapeur (titre) moins élevé (gouttelettes d'eau dans la vapeur). En pratique, quand ce titre baisse la conversion chaleur / travail se fait moins bien. Les turbines ne supportent pas un titre < 0,85 (choc des gouttelettes sur les aubages).

Une autre limite à la baisse de pression du condenseur est le volume de la vapeur : Voir ci contre la courbe du volume de 1 kg de vapeur en fonction de la pression (vapeur de titre 1 sans surchauffe : sur la ligne bleue du diagramme). Cette courbe est tirée de ce site . Valeurs numériques : à 20 b, 10g de vapeur occupent environ 1 litre, 17 litres à 1 b, 147 litres à 100 mb, 282 litres à 50 mb. Plus on baisse la pression du condenseur, plus le volume de vapeur basse pression augmente. Ce qui augmente le volume des pistons (donc les pertes par frottement) ou la taille des turbines (limite de vitesse en extrémité des pales, tenue des matériaux), les vitesses de la vapeur dans les tuyaux avec des risques de laminage, ...

Valeurs numériques pour différents réglages d'une machine parfaite (énergie par kg de vapeur) :

• Cycle de Hirn ci dessus :
  chaleur pour passer de 50 à 400°C : 3046 kj, chaleur au condenseur : 2082 kj
  travail récupéré : 964 kj d'où un rendement de 31,6 %
  (titre de la vapeur au point 3 : 0,87 : 87 % du poids en vapeur)

• Condensation à 1 bar :
  Si au lieu de condenser à 120 mb on choisit 1 b à 100°C :
  on voit sur le diagramme que si le trait liant1 à 3 remonte, les surfaces rouge et verte diminuent et la bleue augmente :
  chaleur pour passer de 100 à 400°C : 2834 kj, chaleur au condenseur : 2178 kj
  travail récupéré : 656 kj d'où un rendement de 23 %
  (titre de la vapeur au point 3 : 0,96)

• Échappement libre :
  Si échappement libre à1 b, il faut chauffer de 20 à 400°C : 3169 kj
  le travail reste le même d'où un rendement de 20 %.

• Variation pression admission (chaudière) :
  Si on baisse la pression du point 2 à 10 b 300°C (sur même verticale au dessus du point 3), le rendement passe de 31,6 à 27 %.
  Si on augmente la pression du point 2 à 40 b 516°C (sur même verticale au dessus du point 3), le rendement passe de 31,6 à 36 %.

Remarque rendement :
Je parle d'une machine parfaite qui suit le cycle de Hirn pour machine à vapeur (décrit ci-dessus).
Une machine parfaite qui suivrait un cycle de Carnot (2 isothermes et 2 isentropiques : un rectangle sur le diagramme TS) entre 50°C et 400°C aurait un rendement supérieur (c'est le rendement moteur maxi possible entre ces 2 sources de chaleur) :
rendement maxi = 1 - Température source froide / Température source chaude = 1 - (50 + 273,15) / (400 + 273,15) = 52 %

Machine réelle Pour une machine réelle, le point 3 est décalé vers la droite en 3r. La surface jaune est à retirer du travail de la machine parfaite (vert) et à ajouter à la chaleur perdue dans condenseur (bleu). La chaleur dépensée (rouge) ne changeant pas et le travail récupéré diminuant (vert - jaune) le rendement de la machine réelle est plus faible.

Laminage

Machine parfaite :

Laminage à l'admission :
Si la vapeur est laminée, par exemple en passant par le régulateur entrouvert (robinet d'admission de vapeur sur les locomotives) ou le tiroir d'une machine à pistons en début d'admission, sa pression chute. Dans l'exemple ci contre, on passe du point 2 en 2' de 20b à 10b.
La vapeur contient la même quantité d'énergie (même surface bleue+verte sous la courbe 20b jusqu'au point 2 que sous la courbe 10b jusqu'au point 2') mais sa "qualité" est moindre. En effet le point 2' est plus à droite que 2, donc la surface bleue indiquant la chaleur au condenseur sera plus grande et donc le travail de la vapeur et le rendement moindre.
Valeurs numériques : si on reprend l'exemple ci dessus (machine parfaite) :
avec condenseur à 50°C le rendement passe de 31 à 28 %
en échappement libre le rendement passe de 20 à 17 %
Laminage à l'échappement :
Si la vapeur est laminée à l'échappement, par exemple par le tiroir d'une machine à pistons ou par un serrage trop fort de l'échappement sur une locomotive, on voit sur le diagramme que le trait liant 1 à 3 remonte (pression et température plus élevées) et donc le travail de la vapeur et le rendement diminuent.
Valeurs numériques : si on reprend l'exemple ci dessus (machine parfaite) :
si l'échappement libre passe de 1b à 2b le rendement passe de 20 à 17 %.

Machine rélle :

Admission :
En 2' la vapeur est plus surchauffée (plus sèche). Ainsi en fin de détente il y a moins de vapeur condensée au point 3' qu'au point 3 (ci contre, la vapeur est sèche en 3'). Dans une machine réelle, la conversion d'énergie est meilleure avec de la vapeur sèche (donc le rendement supérieur).
Le laminage réduit également le débit de vapeur consommée.
Echappement :
Dans une machine réelle à pistons, le laminage à l'échappement crée une contre pression sur le piston qui provoque un travail résistant (le rendement diminue beaucoup plus que sur une machine parfaite).
En pratique le laminage à l'admission est moins pénalisant que celui à l'échappement

Centrale nucléaire PWR 1300 MW Le réacteur chauffe de l'eau sous pression à 155 b et 300°C : c'est le circuit primaire. Cette eau permet de produire de la vapeur dans le circuit secondaire qui n'est pas en contact avec des matières radioactives. Le diagramme ci contre décrit le circuit secondaire : de 1 à 2 : production de vapeur non surchauffée à 70 b, 285°C de 2 à 3 : détente dans turbine haute pression jusqu'à 10 b, 180°C de 3 à 4 : surchauffe vapeur jusqu'à 10 b, 267°C de 4 à 5 : détente dans turbines moyenne et basse pression jusqu'à 56 mb 35°C. A ce point il y a 87 % de vapeur (titre = 0.87). de 5 à 1 : condensation puis pompage de l'eau jusqu'à 70 b. Rendement cycle réel 34 %. Rendement machine parfaite 37 % (cas où les transformations 2 - 3 et 4 - 5 serait des droites verticales). Si en été la température du condenseur monte à 50 °C le rendement réel diminue à 31 % (29 % si 60°C). Dans ce cas la ligne 1 - 5 remonte et donc le travail de la vapeur et le rendement diminuent. Pour l'EPR le point 2 remonte à 78 b, 296°C et le rendement à 37 %. Rapport de la commission Ampère décrivant ce cycle : Rapport Ampère

Centrale électrique à flamme Même type de cycle que précédemment mais avec des températures et des pressions plus élevées. Au point 2 la vapeur est surchauffée puis elle est surchauffée à nouveau au point 4. Rendement de l'ordre de 40 %. Il existe des centrales hypercritiques à 250 b (courbe orange pointillé) qui utilise de la vapeur à une pression supérieure à la pression critique de l'eau (224 bars). Dans ce cas il peut y avoir deux resurchauffes. Rendement jusqu'à 45 %. Soutirage Pour améliorer le rendement, on peut utiliser de la vapeur qui à déjà travaillée pour chauffer l'eau. 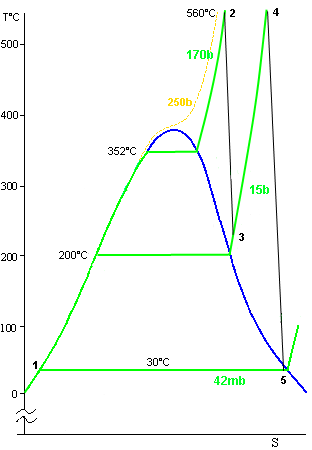Par exemple pour chauffer l'eau au point 1, on prend un peu de vapeur dans la turbine BP, à une température un peu supérieure qui, en ce condensant, chauffe l'eau (en poids, il faut peu de vapeur pour chauffer l'eau). Cette vapeur à déjà fourni du travail : ce qui représente un gain par rapport à la chaleur de la chaudière qui n'a pas travaillée. Puis on prélève (soutire) de la vapeur un peu plus chaude... ainsi de suite jusqu'à une température proche de celle de la chaudière. On a intérêt à faire beaucoup d'étapes, car plus on monte en pression (ou température) moins la vapeur a travaillé (si on prend la vapeur de la chaudière, on ne gagne rien). Dans la pratique il y a jusqu'à une dizaine de soutirages (pour les centrales pwr, le soutirage atteint plus de 30% en poids de la vapeur sortie de la chaudière).

Rendements de machines parfaites

Le graphique ci dessous représente le rendement d'une machine parfaite (rendement maxi) en fonction de la pression relative (pression manomètre) et pour différentes températures de condenseur (40 °C au départ). La gamme de pression correspond aux premières machines à vapeur (0.3 b machine de Watt, machines 1ère moitié du 19ème siècle de 2 à 5 b, ensuite machines à pistons jusqu'à 20 b).

Voir le fichier excel : Fichier excel

Anciennes machines à pistons

On peut résumer l'évolution des rendements des machines à pistons (cf Jacques PAYEN dans Histoire générale des techniques tome IV) :
1712 : machine de Newcomen : estimation de consommation de 16 à 20 kg de charbon par cheval heure (rendement 0,5 %).
1777 : machine de Watt divise la consommation par 4 : 4 à 5 kg charbon / ch h (rendement autour de 2 %)
1870 : nouvelle division par 4 : un peu plus de 1 kg charbon / ch h (rendement 9 %)
1870 - 1914 : division par seulement 1/4 : 750 g charbon / ch h (rendement 12 %) : on atteint les limites de cette technologie, il faut passer aux turbines.

On peut voir le rendement de différentes machines (sources puisées dans des ouvrages spécialisés) dans le
fichier Fichier excel.
Le rendement de ces machines dépasse rarement les 20 %.
Page pour convertir les unités d'énergie (kwh, kcal, kj, kg charbon / ch h) : convertisseur.

Leurs rendements sont limités pour plusieurs raisons :

• Effet de paroi :
  En fin d'échappement, les parois du cylindre sont à une température proche de celle du condenseur (p ex 40°C). Lors de l'admission suivante, la vapeur chaude (200°C pour 14b) va se condenser sur les parois, d'où une perte de puissance (en plus les surfaces mouillées conduisent mieux la chaleur de la vapeur !!).
  Si la surface est encore mouillée lors de l'échappement, l'évaporation qui s'en suit va refroidir les parois.
  L'utilisation de la vapeur surchauffée diminue ce problème, car elle permet de réchauffer les parois sans condensation. Ainsi la surchauffe améliore nettement le rendement pratique (le manuel de l'ingénieur de locomotive Henschel indique une économie en charbon de 21 % pour une surchauffe à 400°C). Cette amélioration pratique est très supérieure à celle théorique sur une machine parfaite (cf ci_dessus).
  On peut aussi chauffer les parois : on fait circuler de la vapeur dans des enveloppes autour des cylindres pour éviter les condensations. Les pertes de chaleurs des enveloppes vers l'extérieur sont largement compensées par l'augmentation du rendement dans les cylindres.

• Espace mort :
  Quand le piston est en fin de course, il y a un espace entre le piston et le fond du cylindre. Ce volume, ajouté à celui de la conduite qui relie le fond de cylindre au tiroir est appelé espace mort. Au début de l'admission, ce volume est rempli de vapeur qui ne travaille qu'en participant à la détente (elle ne bouge pas directement le piston). Cette vapeur travaille moins, d'où une perte à chaque cycle.
  Les constructeurs essaient de diminuer au maximum ces espaces morts (P ex : les machines Corliss avec des tiroirs rotatifs directement au fond du cylindre, sans conduit).

• On peut ajouter une limite en température pour assurer le graissage.

• Une limite en pression car les petites fuites des organes de distribution génèrent des pertes importantes en haute pression.

• Une limite en pression du condenseur (trop grand volume de vapeur si basse pression).

Voir page Histoire des machines à vapeur : amélioration du rendement

Machines à plusieurs expansions :
Pour diminuer les problèmes décrits ci_dessus, on détend la vapeur dans plusieurs cylindres en cascade (haute pression, puis moyenne pression puis basse pression). L'échappement de l'étage précédant sert d'admission de l'étage en cours. Ainsi il y a moins d'effet paroi car la chute de température est répartie : la température varie moins dans chaque cylindre. De même, le cylindre hp est plus petit, son espace mort l'est aussi.
Ces machines obtiennent ainsi un meilleur rendement.
En caricaturant, si on fait beaucoup d'étages on obtient une turbine  !!

Modèles réduits : effet d'échelle

Pour faire un modèle réduit, si on divise toutes les cotes par la même échelle, sa forme ressemblera à l'original mais qu'en est-il des caractéristiques physiques ? Prenons par exemple une réduction au dixième : les cotes sont divisées par 10. Les surfaces par 10 au carré donc par 100. Les volumes (donc aussi les masses) par 10 au cube donc par 1000.
Le volume du cylindre diminue plus que sa surface, ce qui accroît les effets de paroi et donc diminue le rendement.
La résistance des matériaux dépend de la surface (ex section d'une bielle, ...). La rigidité (rapport résistance (liée à la surface) sur masse (volume)) est améliorée.
Le volume diminue plus que la section des tuyaux et des lumières de distribution, donc la vitesse de la vapeur et le laminage diminuent.
La masse en mouvement (inertie) diminue plus que le diamètre des roues, ce qui autorise théoriquement des vitesses plus élevées (diminution de l'effet de paroi d'où meilleur rendement).

Pour aller plus loin : sites intéressants

Cours de thermodynamique : nte.enstmac.Ce site fournit également le simulateur décrit ci dessous.
Thermodynamique appliquée : thermoptim. Contient un extrait de livre en pdf intéressant : CentralesVapeur.pdf
Modèlisme : La Confrérie de Amateurs de Vapeur (CAV) : cav-escarbille.com.

Utilisation simulateur

Sur ce site internet de simulation on peut calculer les différents points des diagrammes T S :
-Les températures sont en K (kelvin) = T °C + 273.
-Les pressions sont des pressions absolues (manomètre + 1b) en Pa (pascal) = P en bars * 100000 = P en mb * 100.
-Enthalpie en kj / kg (j'utiliserai le symbole H dans ce qui suit).
Au cours d'une transformation à pression constante (donc sans production de travail dans une machine), la différence d'enthalpie du fluide entre la fin et le début donne la quantité de chaleur échangée. Par exemple si on prend le diagramme T S du début, la chaleur consommée (surface rouge) est égale à l'enthalpie au point 2 (H2) moins l'enthalpie au point 1 (H1). De même la surface bleue = H3 - H1.
Au cours d'une transformation avec production de travail dans une machine et sans échange de chaleur, la différence d'enthalpie du fluide entre le début et la fin donne la quantité de travail fournie. Par exemple si on prend le diagramme T S du début, le travail fourni par la  vapeur est H2-H3. C'est également vrai pour une machine réelle bien isolée (pas d'échange de chaleur) travail = H2-H3r.

Exemple de calcul du diagramme T S du début :
Se connecter au site : au centre on reconnaît le diagramme T S.
Dérouler le menu "Choix de calcul" (cliquer sur la flèche vers le bas à coté) et choisir "température et tire de vapeur"
Une petite fenêtre apparaît : entrer température= 323 (en kelvin=50+273) et titre = 0 (eau sans vapeur : point sur la courbe bleue de gauche). Cliquer sur le bouton "placer le point".
Après calcul, le point apparaît sur les diagrammes et les résultats s'affichent dans la fenêtre "Sorties numériques" (pour ouvrir cette fenêtre dérouler le menu "Fenêtres"). On note H1=215 kj/kg
Dérouler le menu "Choix de calcul" et choisir "Température et pression"
Entrer température= 673 (en kelvin=400+273) et pression = 2000000 (en Pa=20b*100000) puis Cliquer sur le bouton "placer le point".
Dans la fenêtre "Sorties numériques" on note H2=3261 kj/kg et l'entropie S2=7170 j/kg/K.
Dans une machine parfaite l'entropie reste constante lors de la transformation 2 -> 3 (verticale dans le diagramme T S) ce qui permet de calculer le point 3 :
Dérouler le menu "Choix de calcul" et choisir "Température et entropie"
Entrer température= 323 (en kelvin=50+273) et entropie S3=S2=7170 j/kg/K puis Cliquer sur le bouton "placer le point".
Dans la fenêtre "Sorties numériques" on note H3=2297 kj/kg.
Chaleur dépensée = H2-H1=3046 kj/kg.
Travail récupéré = H2-H3=964 kj/kg.
Chaleur condenseur = H3-H1=2082 kj/kg.